In this scenario, we have a binary mediator \(M\), a binary outcome \(Y\), and no effect modification. The sample size is 50 and there are 3 covariates.
Sample simulated Dataset
dat <- cma_sampledata(N = 50, L=3, P=3, scenario=2, seed=7)
head(dat$data, n = 3L)
#> z1 z2 z3 M x1 x2 x3 y
#> 1 2.2767428 0.1432685 0.7973699 1 -0.3556944 2.02334405 -1.477592 1
#> 2 -1.0893537 -0.0944783 0.4035083 0 1.0973004 0.86249250 -2.973256 1
#> 3 -0.6389109 0.2491581 -0.1243989 0 -0.9066920 -0.02490949 -1.339762 0
dat = dat$dataFit BKMR Models
let \(A\) be a \(n\)-by-\(L\) matrix containing an exposure mixture
comprised of \(L\)
elements,E.M and E.Y be effect modifiers of
exposure-mediator and exposure-outcome relationship respectively, \(y\), a vector of outcome data, and \(m\), a vector of mediator data.
Z.M <- cbind(A,E.M)
Z.Y <- cbind(A,E.Y)
Let Z.M be the exposures and effect modifers
E.M and let Z.Y be the exposures and effect
modifers E.Y, create one more matrix containing the
exposures, effect modifier Z.Y and mediator, precisely in
that order.
Zm.Y <- cbind(Z.Y,m)
NOTE: the last column of the Zm.Y matrix must
be your mediator in order for the functions to work properly.
A <- cbind(dat$z1, dat$z2, dat$z3)
X <- cbind(dat$x1, dat$x2, dat$x3)
y <- dat$y
m <- dat$M
E.M <- NULL
E.Y <- dat$x2
Z.M <- cbind(A,E.M)
Z.Y <- cbind(A, E.Y)
Zm.Y <- cbind(Z.Y, m)
set.seed(1)
fit.y <- kmbayes(y=y, Z=Zm.Y, X=X, iter=10000, verbose=TRUE, varsel=FALSE)
#save(fit.y,file="bkmr_y.RData")
set.seed(2)
fit.y.TE <- kmbayes(y=y, Z=Z.Y, X=X, iter=10000, verbose=TRUE, varsel=FALSE)
#save(fit.y.TE,file="bkmr_y_TE.RData")
set.seed(3)
fit.m <- kmbayes(y=m, Z=Z.M, X=X, iter=10000, verbose=TRUE, varsel=FALSE)
#save(fit.m,file="bkmr_m.RData")Values at which to predict counterfactuals
Mean level of confounders:
We define the change in exposure for which you want to estimate the
mediation effects: in this example, we will consider a change in all
exposures from their 25th to 75th percentiles, fixing age
(E.Y) at testing to its 10th and 90th percentiles. However,
this contrast can be anything.
Note: If modifiers are considered, you should fix the levels of the modifiers
astar <- c(apply(A, 2, quantile, probs=0.25))
a <- c(apply(A, 2, quantile, probs=0.75))
e.y10 = quantile(E.Y, probs=0.1)
e.y90 = quantile(E.Y, probs=0.9)The index of the MCMC iterations to be used for inference:
sel<-seq(5000,10000,by=10)Estimate TE for BKMR
Estimate the TE for a change in the exposures from \(a^*\) to \(a\) fixing Effect modifier at testing to its 10th percentile or 90th percentile:
e.y10 = quantile(E.Y, probs=0.1)
e.y90 = quantile(E.Y, probs=0.9)
TE.ey10 <- TE.bkmr(a=a, astar=astar, e.y = e.y10, fit.y.TE=fit.y.TE, X.predict=X.predict, alpha=0.05, sel=sel, seed=122)
TE.ey90 <- TE.bkmr(a=a, astar=astar, e.y = e.y90, fit.y.TE=fit.y.TE, X.predict=X.predict, alpha=0.05, sel=sel, seed=122)Look at the posterior mean, median, and 95% CI for TE:
TE.ey10$est
#> mean median lower upper sd
#> TE 0.3241404 0.3244238 0.01677121 0.6159663 0.1536497
TE.ey90$est
#> mean median lower upper sd
#> TE 0.430469 0.4243573 0.07051303 0.7911519 0.1731175
plotdf <- as.data.frame(TE.ey10$est)
plotdf["Effect"] <- rownames(plotdf)
ggplot(plotdf, aes(Effect, mean, ymin = lower, ymax = upper)) +
geom_pointrange(position = position_dodge(width = 0.75)) + coord_flip()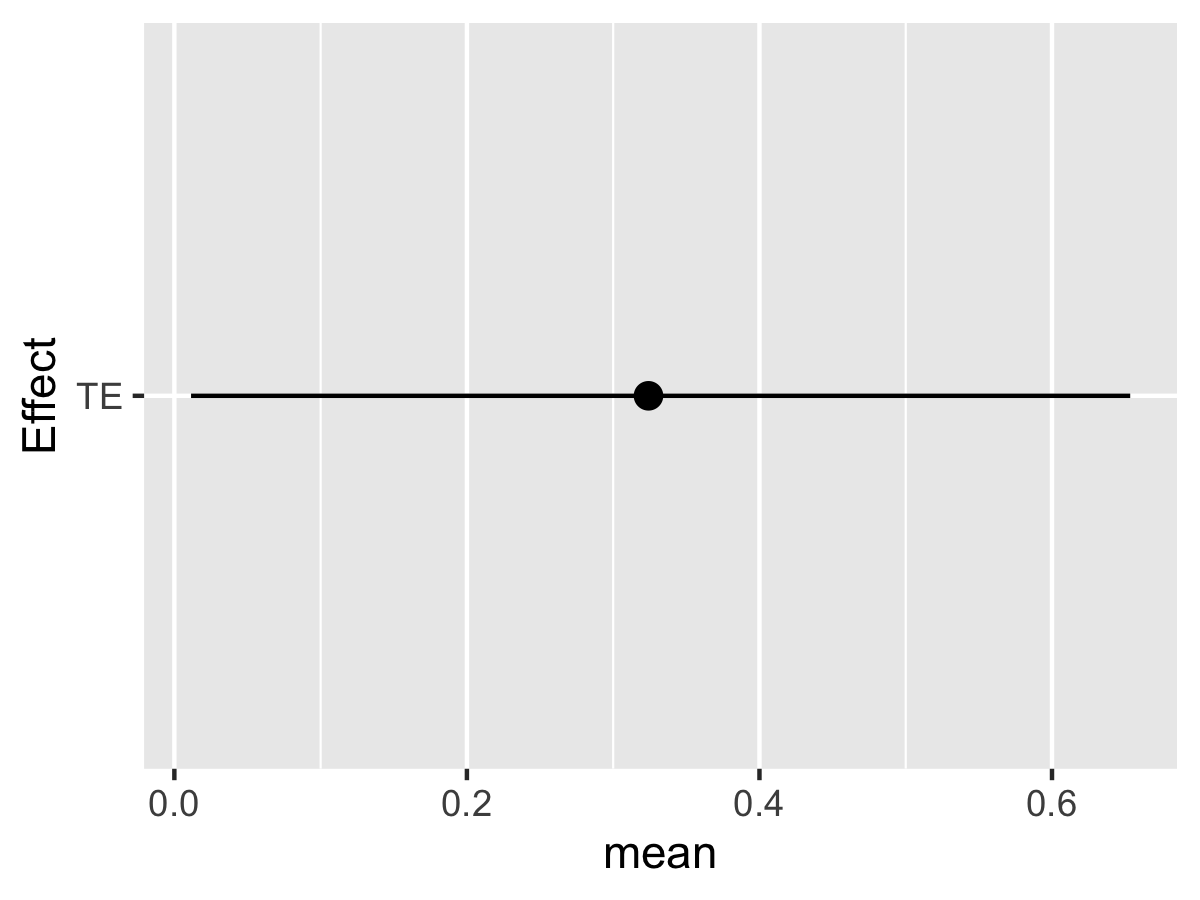
Estimate CDE for BKMR
Estimate the CDE for a change in the exposures from \(a^*\) to \(a\), fixing the mediator at its 10th, 50th, and 75th percentile and the effect modifier at testing at its 10th percentile:
CDE.ey10 <- CDE.bkmr(a=a, astar=astar, e.y = e.y10, m.quant=c(0.1,0.5,0.75), fit.y=fit.y, alpha=0.05, sel=sel, seed=777)
#> [1] "Running 3 mediator values for CDE:"
#> [1] "1 out of 3"
#> [1] "2 out of 3"
#> [1] "3 out of 3"
CDE.ey90 <- CDE.bkmr(a=a, astar=astar, e.y = e.y90, m.quant=c(0.1,0.5,0.75), fit.y=fit.y, alpha=0.05, sel=sel, seed=777)
#> [1] "Running 3 mediator values for CDE:"
#> [1] "1 out of 3"
#> [1] "2 out of 3"
#> [1] "3 out of 3"Look at the posterior mean, median, and 95% CI for the CDEs:
CDE.ey10$est
#> mean median lower upper sd
#> CDE10% 0.3092927 0.2999788 -0.043365129 0.6917523 0.1796301
#> CDE50% 0.3609607 0.3402882 -0.005062313 0.7992176 0.1939582
#> CDE75% 0.3609607 0.3402882 -0.005062313 0.7992176 0.1939582
CDE.ey90$est
#> mean median lower upper sd
#> CDE10% 0.4085146 0.4027476 0.02286425 0.8323147 0.2007848
#> CDE50% 0.4562550 0.4515731 0.08655578 0.9197106 0.2095806
#> CDE75% 0.4562550 0.4515731 0.08655578 0.9197106 0.2095806Plotting:
plotdf <- as.data.frame(CDE.ey10$est)
plotdf["Effect"] <- rownames(plotdf)
ggplot(plotdf, aes(Effect, mean, ymin = lower, ymax = upper )) +
geom_pointrange(position = position_dodge(width = 0.75)) + coord_flip()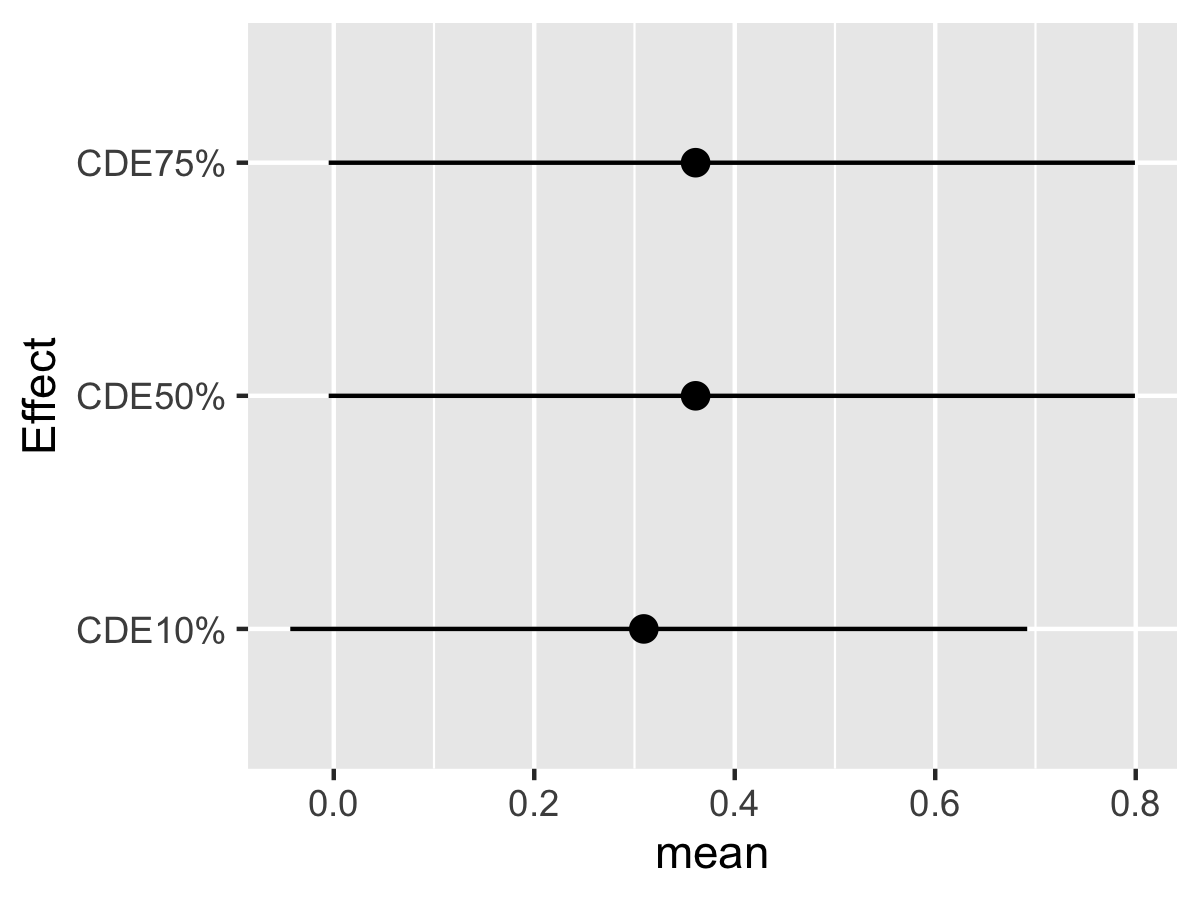
Estimate NDE/NIE for BKMR
Estimate the TE, NDE and NIE for a change in the exposures from \(a^*\) to \(a\) fixing age at testing to its 90th percentile.
Note: this step takes a while to run and will take longer for more
complex BKMR fits, longer sel vectors and larger.
mediationeffects.ey10 <- mediation.bkmr(a=a, astar=astar, e.y = e.y10, fit.m=fit.m, fit.y=fit.y, fit.y.TE=fit.y.TE, X.predict.M=X.predict, X.predict.Y=X.predict, alpha=0.05, sel=sel, seed=22, K=10)
mediationeffects.ey90 <- mediation.bkmr(a=a, astar=astar, e.y = e.y90, fit.m=fit.m, fit.y=fit.y, fit.y.TE=fit.y.TE, X.predict.M=X.predict, X.predict.Y=X.predict, alpha=0.05, sel=sel, seed=22, K=10) Look at the posterior mean, median, and 95% CI for the TE, NDE, and NIE
mediationeffects.ey10$est
#> mean median lower upper sd
#> TE 0.30916635 0.314290915 -0.02660571 0.5727188 0.1549434
#> NDE 0.29834270 0.301233360 -0.33291485 0.9103089 0.3239850
#> NIE 0.01082364 0.004102463 -0.59770537 0.6713659 0.3193340
#> CDE10% 0.28813715 0.295343850 -0.10165967 0.6682970 0.1904052
#> CDE50% 0.34321913 0.342000447 -0.04373672 0.7398543 0.1917391
#> CDE75% 0.34321913 0.342000447 -0.04373672 0.7398543 0.1917391
mediationeffects.ey90$est
#> mean median lower upper sd
#> TE 0.415301283 0.40574600 0.11468494 0.7543082 0.1656023
#> NDE 0.422781310 0.40948509 -0.27526006 1.1759479 0.3487023
#> NIE -0.007480027 -0.01404017 -0.74070549 0.7414162 0.3649172
#> CDE10% 0.386433102 0.39061531 -0.03306667 0.8217995 0.2082319
#> CDE50% 0.437912375 0.43447120 0.05164739 0.8499772 0.2022834
#> CDE75% 0.437912375 0.43447120 0.05164739 0.8499772 0.2022834Plotting
plotdf <- as.data.frame(mediationeffects.ey10$est)
plotdf["Effect"] <- rownames(plotdf)
ggplot(plotdf, aes(Effect, mean, ymin = lower, ymax = upper )) +
geom_pointrange(position = position_dodge(width = 0.75)) + coord_flip()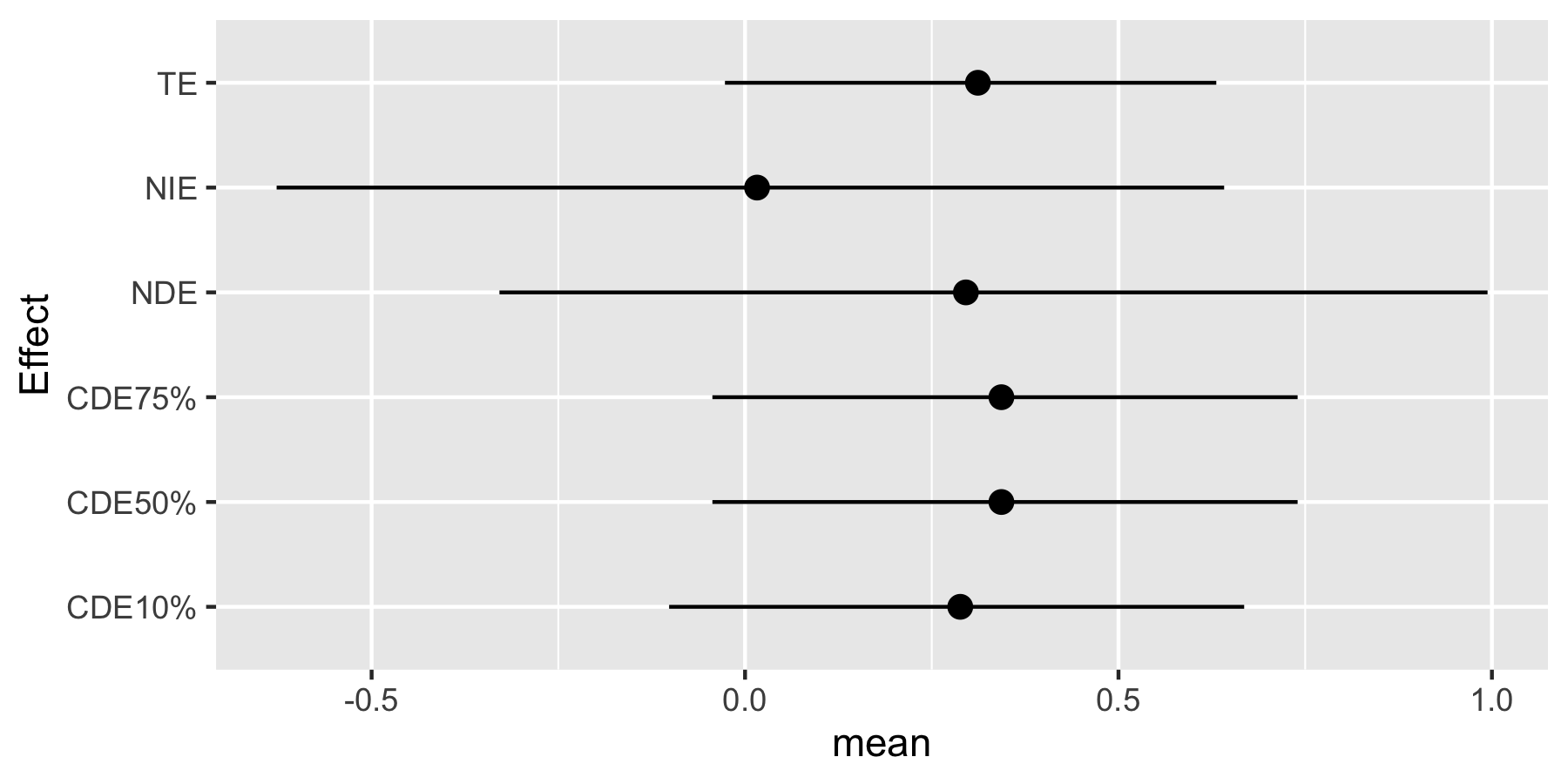
Summary statistics of the predictor-response function
Risk Summary For Totel Effect
riskSummary10 = TERiskSummaries.CMA(fit.TE = fit.y.TE, e.y=e.y10, e.y.name = "E.Y", sel=sel)
ggplot(riskSummary10,
aes(quantile,
est,
ymin = est - 1.96 * sd,
ymax = est + 1.96 * sd)) +
geom_pointrange()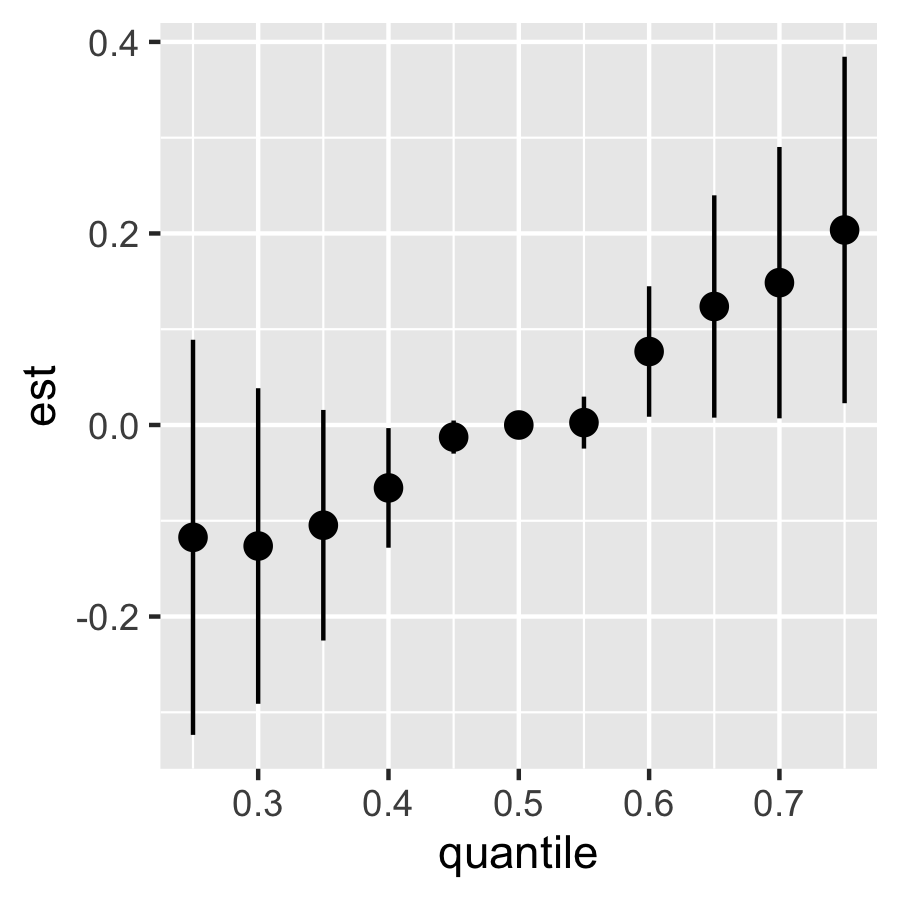
riskSummary90 = TERiskSummaries.CMA(fit.TE = fit.y.TE, e.y=e.y90, e.y.name = "E.Y", sel=sel)
ggplot(riskSummary90,
aes(quantile,
est,
ymin = est - 1.96 * sd,
ymax = est + 1.96 * sd)) +
geom_pointrange()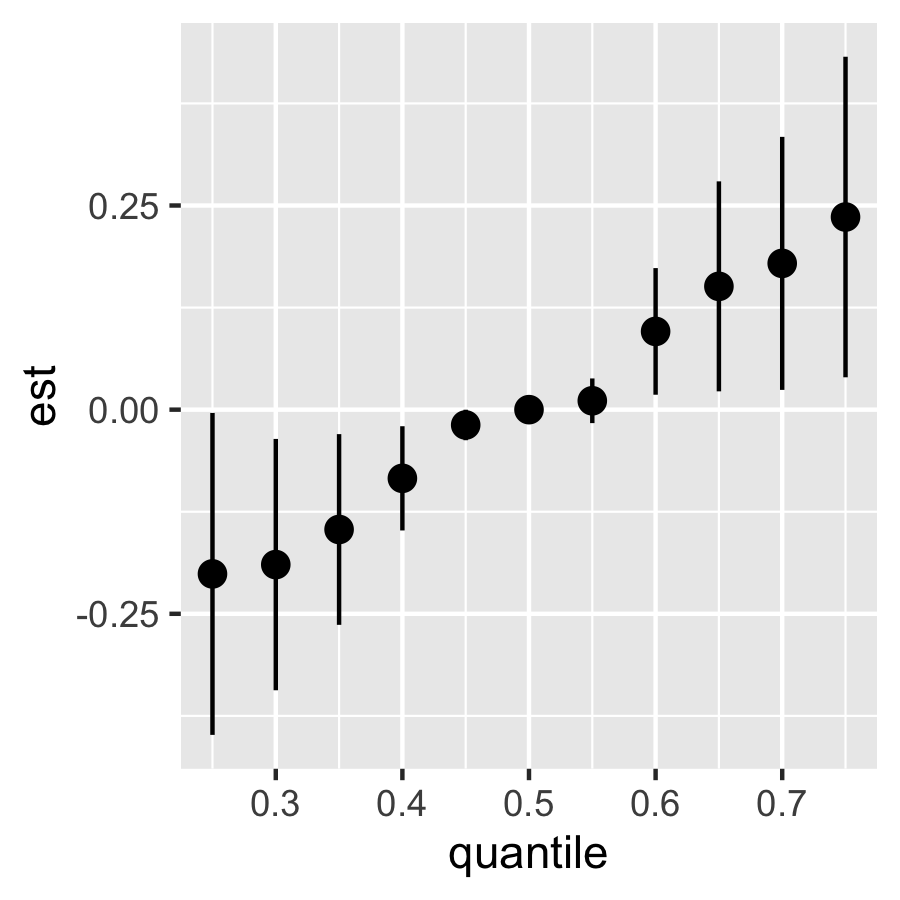
Since there’s no effect modification, the two above figures are similar.
Risk Summary For Controlled Direct Effect
# CDE
CDEriskSummary10 = CDERiskSummaries.CMA(fit.y = fit.y, e.y = e.y10, e.y.name = "E.Y", m.name = "m", sel = sel)
ggplot(CDEriskSummary10, aes(quantile, est, ymin = est - 1.96*sd,
ymax = est + 1.96*sd, col = m)) +
geom_pointrange(position = position_dodge(width = 0.75))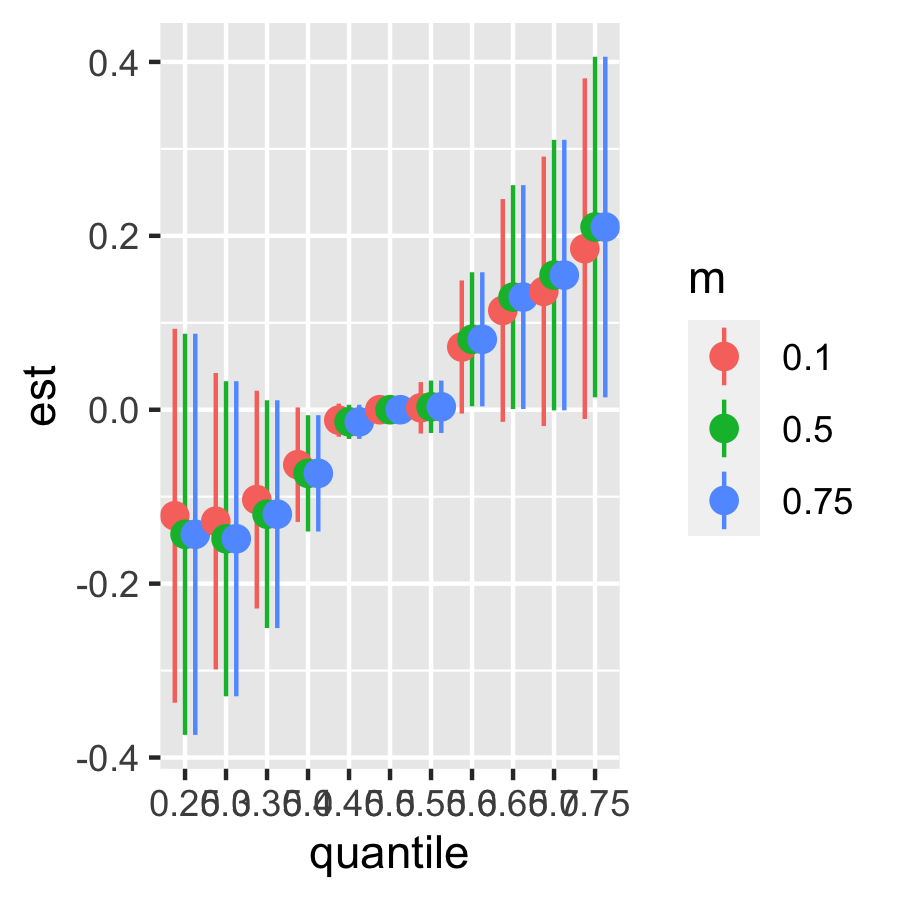
CDEriskSummary90 = CDERiskSummaries.CMA(fit.y = fit.y, e.y = e.y90, e.y.name = "E.Y", m.name = "m", sel = sel)
ggplot(CDEriskSummary90, aes(quantile, est, ymin = est - 1.96*sd,
ymax = est + 1.96*sd, col = m)) +
geom_pointrange(position = position_dodge(width = 0.75))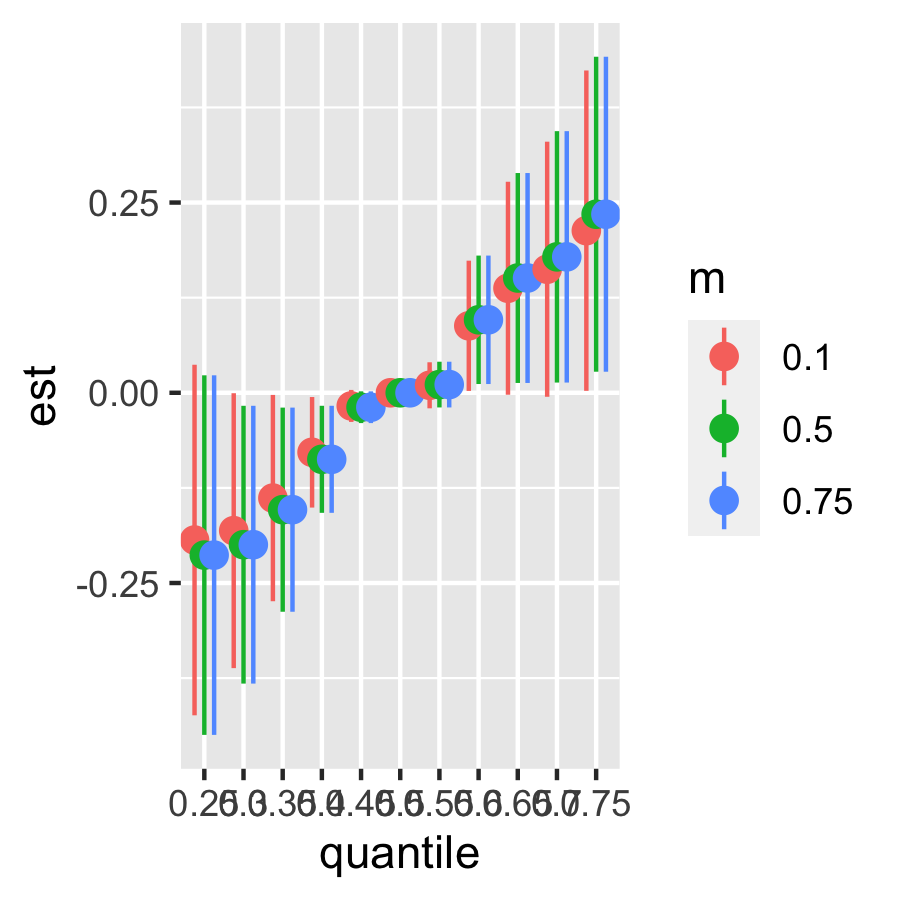
Since there’s no effect modification, the two above figures are similar. ## Single-predictor health risks
Total Effect
risks.singvar10 = SingVarRiskSummaries.CMA(BKMRfits = fit.y.TE, which.z = 1:3,
e.y=e.y10, e.y.names="E.Y",
sel=sel)
plot_singvar10 <- ggplot(risks.singvar10, aes(variable, est, ymin = est - 1.96*sd, ymax = est + 1.96*sd, col = q.fixed)) + theme(legend.position="none")+
geom_pointrange(position = position_dodge(width = 0.5)) +
coord_flip()
risks.singvar90 = SingVarRiskSummaries.CMA(BKMRfits = fit.y.TE, which.z = 1:3,
e.y=e.y90, e.y.names="E.Y",
sel=sel)
plot_singvar90 <- ggplot(risks.singvar90, aes(variable, est, ymin = est - 1.96*sd, ymax = est + 1.96*sd, col = q.fixed)) +
geom_pointrange(position = position_dodge(width = 0.5)) +
coord_flip()
ggarrange(plot_singvar10, plot_singvar90, ncol=2, nrow=1)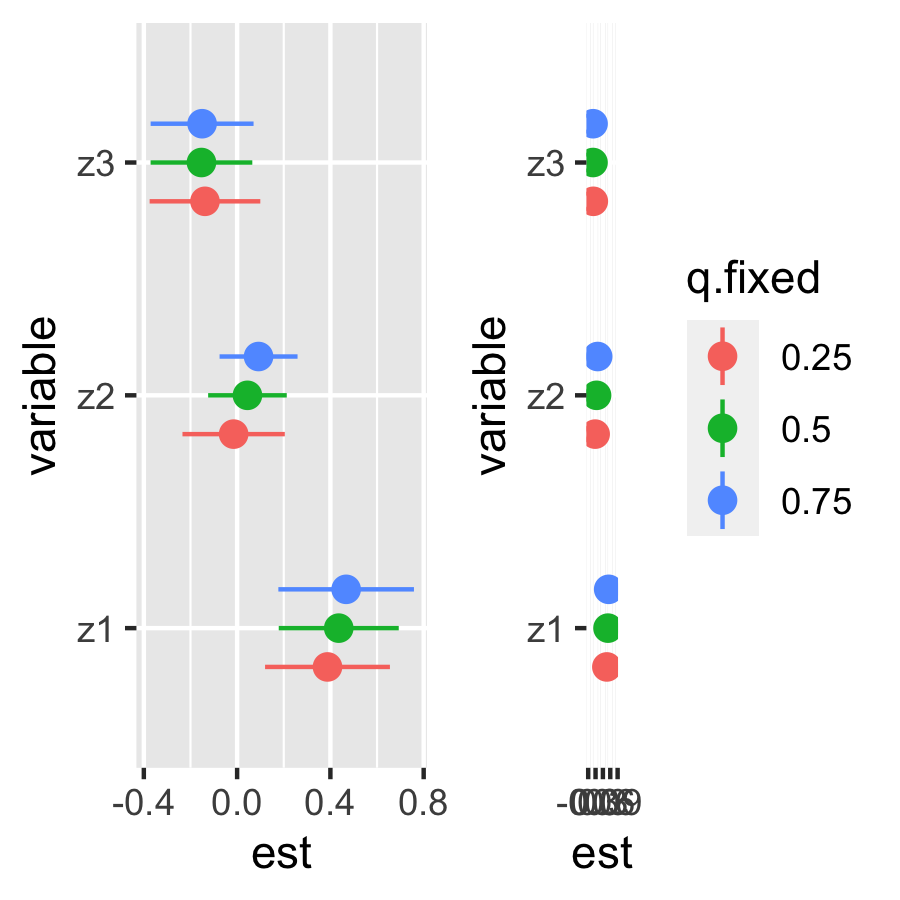
Since there’s no effect modification, the two above figures are similar.
Controlled Direct Effect
CDErisks.singvar10 = CDESingVarRiskSummaries.CMA(BKMRfits = fit.y,
e.y=e.y10, e.y.names="E.Y", m.name = "m",
sel=sel)
plotCDE10 <- ggplot(CDErisks.singvar10, aes(variable, est, ymin = est - 1.96*sd,
ymax = est + 1.96*sd, col = q.fixed, linetype = m.fixed)) +
geom_pointrange(position = position_dodge(width = 0.5)) +theme(legend.position="none")+
coord_flip()
CDErisks.singvar90 = CDESingVarRiskSummaries.CMA(BKMRfits = fit.y,
e.y=e.y90, e.y.names="E.Y", m.name = "m",
sel=sel)
plotCDE90 <- ggplot(CDErisks.singvar90, aes(variable, est, ymin = est - 1.96*sd,
ymax = est + 1.96*sd, col = q.fixed, linetype = m.fixed)) +
geom_pointrange(position = position_dodge(width = 0.5)) +
coord_flip()
ggarrange(plotCDE10, plotCDE90, ncol=2, nrow =1)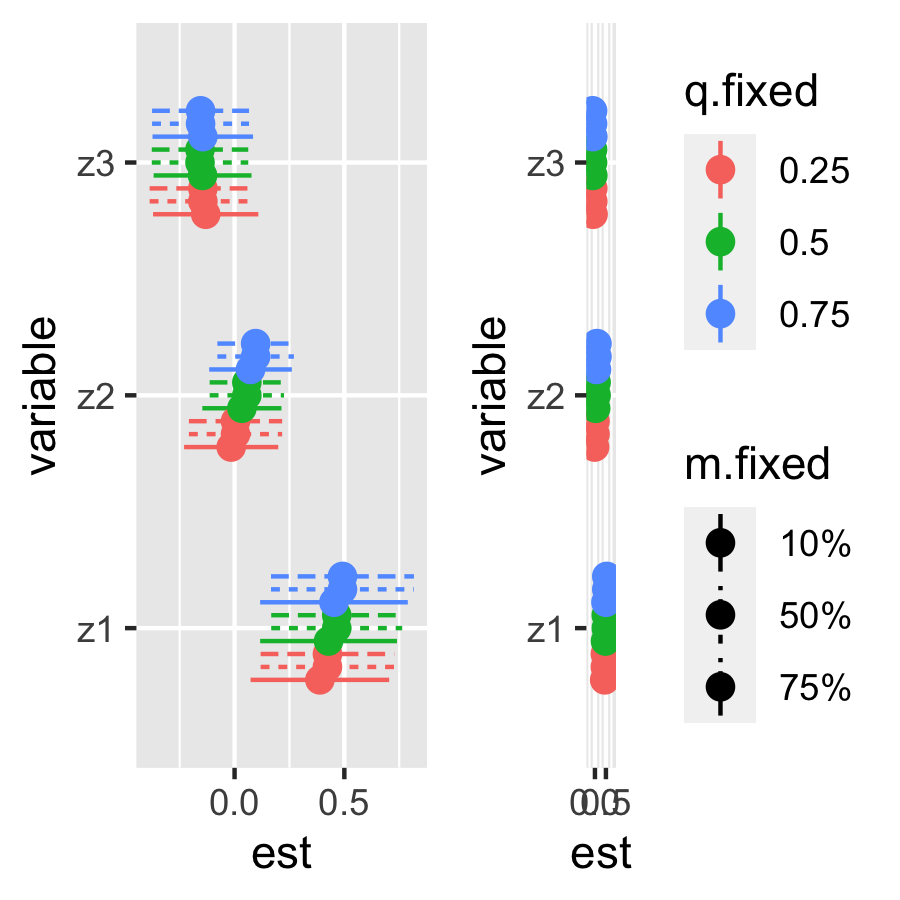
Since there’s no effect modification, the two above figures are similar.